The economic risks involved in drug discovery can prevent drug candidates from progressing into clinical development. Modeling and simulation are important tools in a rational approach to drug discovery and development and can help prioritize and assess the potential of compounds, thereby reducing risk.
The work at FCC aims at delineating and streamlining the modeling and simulation process in model based drug discovery and development to increase both the pace of model development and the predictive power of future models. FCC has worked together with AstraZeneca in a 3-year project to develop new tools and increase usage of advanced modeling and simulation within the Drug Metabolism & Pharmacokinetics and Pharmacokinetics-Pharmacodynamics (PKPD) scientific areas.
Mathematical model based analysis of experimental data on how novel compounds are taken up, distributed, and eliminated, and their pharmacological effect, are used both in preclinical studies as well as in translational science to rationally design dosage regimens for clinical studies. However, the use of already existing data and models to answer questions of integrative character is often under-used. For example, to predict drug effects when scaling from healthy to diseased individuals a meta-analysis of already existing studies can be utilized. Quantification of uncertainty is another important topic where there has been a lack of proper tools and techniques. The dynamics of non-esterified fatty acids (NEFA) in response to administration of nicotinic acid in the rat have served as a test bed to address the objectives of the project.
Industrial Applications and Needs
The increased use of advanced modeling and simulation in PKPD analysis provides means to address the so called 3Rs (replace, refine, reduce), rationally approach the design of biologics to target specific points in mapped out mechanisms, to help characterize pharmacodynamic effects of compounds without systemic exposure, and handle the complexity introduced by systems involving feedback resulting in tolerance and rebound phenomena. These areas are in turn described below and have to varying extent been addressed during the project.
Replace, Reduce, Refine
The iterative cycle of experimental studies complemented by computer simulations are instrumental to implementing any serious 3R strategy. Here, small pilot experiments followed by modeling and simulation provide input to the design of new experiments (dosage, number of individuals, number of sample points, etc) for optimal utilization of resources. This is important since the size and cost of experimental studies increase during the course of a project when moving from pilot exploratory acute PK studies to chronic toxicokinetic studies with a large number of individuals.
Design of Biologics
Models of increasing complexity compared to today’s gallery of standard PKPD models will be needed to characterize the behavior of for example novel biologics. One example is target mediated drug disposition (TMDD) models required to describe the highly nonlinear dose dependence of some ligand-receptor interactions. One may also expect that this type of models, that include biological mechanisms from receptor pharmacology, could be very useful to investigate where and how a novel compound should interact to maximize its effect. This is partly what the emerging field of system pharmacology is expected to be able to deliver.

Dose-Response-Time Analysis
Compounds that exert their effect without entering the circulation (other than possibly as a secondary effect), such as topical delivery, lung disposition, or ocular drug delivery are all examples where models have to be built without the traditional sequential PKPD approach. Here the area of dose-response-time analysis plays an important role, where the traditional PK part is replaced by a bio-phase model feeding into the PD model.
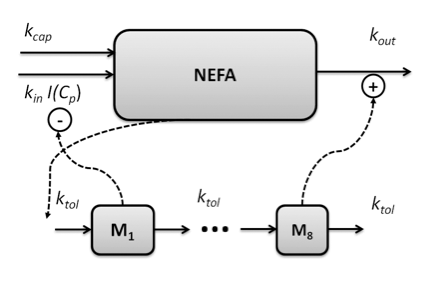
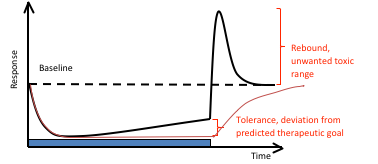
Tolerance Build-up and Rebound
The role of feedback and how to rationally design dosing schedules, minimizing the effect of tolerance build-up and rebound, is also an important field. Mechanistic PKPD models are required to unravel the complexity, and to generate optimal steady state concentration-response relationships, response-time courses and dosing schedules.
Meta-analysis Using Existing PKPD Models and Data
To provide predictions of drug effects when scaling from healthy to diseased individuals, a joint analysis of the data from normal and diseased animals is of interest. For instance, a drug that has proven effective in the normal case may not display the same effect in the disease system, which in turn can lead to underestimation of suitable dose levels. The purpose of the joint analysis carried out during this project was to determine in what way disease affects the pharmacodynamics and to quantify this effect by a combined analysis, where all data sets from both normal Sprague Dawley rats and obese Zucker rats have been used simultaneously. Parameter estimation results from the combined analysis were then compared to a population PKPD analysis previously done separately for each group. The meta-analysis led to the identification of the pharmacodynamic parameters most affected by the disease, which turned out to be the maximum drug-induced inhibitory effect, the plasma concentration at 50 percent reduction of maximal effect (i.e., potency), and the sigmoidicity factor of the drug effect inhibitory function, respectively.
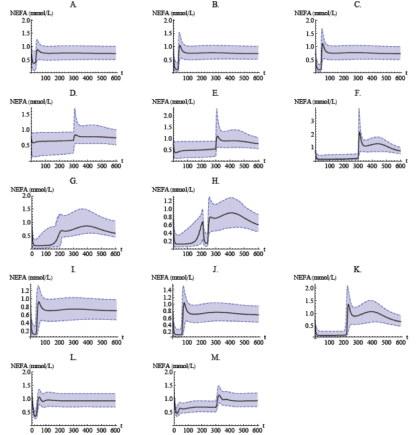
Population model simulation of NEFA plasma concentrations for normal Sprague–Dawley rats after infusion (a–h), oral administration (i–k), for obese Zucker rats after infusion (l–m). Infusion of (a) 1 μmol kg−1; (b) 5 μmol kg−1; (c) 20 μmol kg−1, over 30 min; (d) 5 μmol kg−1; (e) 10 μmol kg−1; (f) 51 μmol kg−1, over 300 min; (g) 5 μmol kg−1 over 30 min followed by a stepwise decrease in infusion rate every 10 min for 180 min; (h) 5 μmol kg−1 over 30 min followed by a stepwise decrease in infusion rate every 10 min for 180 min, and another 5 μmol kg−1 infusion over 30 min. Oral dose of (i) 24 μmol kg−1, (j) 82.1 μmol kg−1, and (k) 812 μmol kg−1. Infusion of (l) 20 μmol kg−1 over 30 min and (m) 51 μmol kg−1 over 300 min. Shaded bands show the Monte Carlo-derived 90% population variability bands.
Model Uncertainty
The vast majority of today’s PKPD models are not able to handle uncertainty in the model dynamics. However, so called nonlinear mixed-effects (NLME) modeling, the current workhorse in PKPD data analysis, allow for variability and uncertainty both within and between subjects being modeled. In this project we have investigated how to also incorporate uncertainty in the model dynamics in NLME modeling. This turns out to provide both more robust estimation methods (modified and regularized likelihood function to be optimized) and the ability to quantify and detect model misspecification.
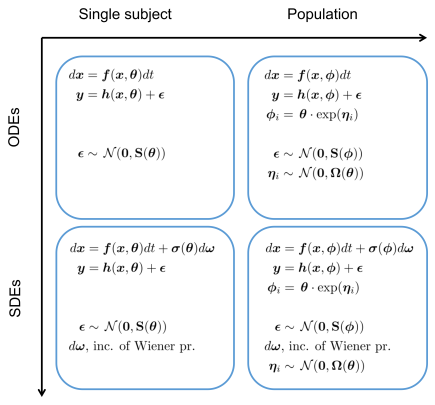
A formal way of specifying uncertainty is through the use of probability distributions. The most common use of concepts from statistics and probability theory in biological applications is to describe variability that stems from the stochastic nature of single reactions, variations between individuals, noise and variability introduced in the process of taking single or repeated measurements, etc. However, probability distributions can also be used to characterize uncertainty in a broader sense, in particular in combination with measurement data. Assigning probability distributions to entities such as parameters, state variables, and system and measurement noise variables in dynamical models of biochemical networks, provides understanding of both the quantity itself and how precisely or uncertainly it is known. This approach becomes even more useful if one not only uses these prior probability distributions and studies their time evolution, but also updates them using time series experimental data to obtain so called posterior distributions. This more elaborate way of representing the system under study naturally comes with the cost of more complex computations and requires more advanced mathematics but the gain of obtaining not only single numerical values for quantities but also some measure of quality or quantified uncertainty is a tremendous advantage. To fully exploit the described methodology there is a need to abandon systems of Ordinary Differential Equations (ODEs), in favor of systems of stochastic differential equations (SDEs). These are more complex mathematical objects than ODEs since they represent not only a single solution trajectory but a family of solutions, so called realizations, whose statistical properties can be captured in terms of time varying distributions for the state variables.
Illustration of different modeling frameworks. The approaches range from a single subject explained by a set of ordinary differential equations to a population of subjects where the underlying dynamics is described by a set of stochastic differential equations (SDE). Note that the differential equations are written in differential form, which is the standard notation for SDEs.
Fixed step length
Fixed step length
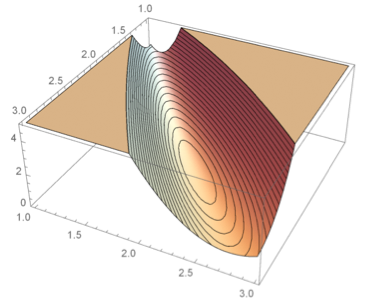
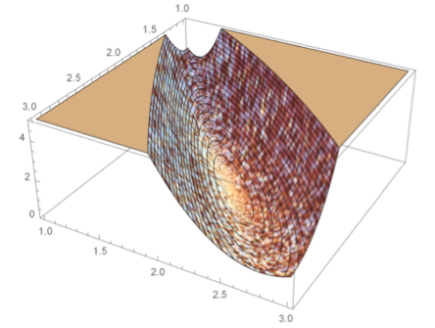
Adaptive methods for numerical integration cause non-smooth behavior of the negative log-likelihood (at small scales).
Improved Estimation Algorithms
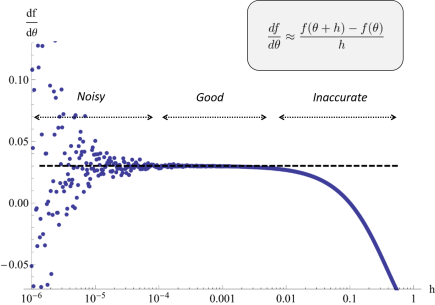
One of the most used methods for parameter estimation in NLME models is maximization of the approximate population likelihood function resulting from the first order conditional expectation approximation. The optimization is performed using efficient gradient-based optimization methods such as the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm. The gradient of the objective function needed by methods such as BFGS is typically computed by finite difference approximations. However, finite difference approximations might become an unreliable description of the gradient due to the numerical solutions of the model equations. Numerical ODE solvers using adaptive step length are known to introduce quantification errors to the objective function, making it non-smooth on small scale. Instead, to overcome such problems, the gradient can be determined by formally differentiating the objective function. To calculate the components of the likelihood gradient with respect to the parameters, one typically needs to solve the so called sensitivity equations of the parameterized differential equations. These equations are obtained by differentiating the system equations with respect to the parameters to be estimated. Not only is the approach of using sensitivity equations more accurate, but it is also generally faster since a lot of likelihood function evaluations are avoided.
We have implemented a sensitivity-equation-based para-meter estimation algorithm, which uses sensitivity equations for determining gradients for both the optimization of individual random effect parameters, and for the optimization of the fixed effect population parameters. Information provided by the sensitivity equations can also be exploited to obtain better initial values for the individual optimization of the random para-meters. The algorithm is applicable to models based on ODEs as well as on SDEs. Because of its high accuracy in determining the gradients, the new algorithm shows more robustness to pre-optimum termination and to converge in situations where current industry-standard software such as NONMEM fails.
A finite difference approximation to a component of the likelihood gradient may be both noisy and inaccurate depending on the choice of perturbation scale. In the worst case, different perturbations may be needed for different components. Sensitivity based gradient computations can resolve the problem.
A finite difference approximation to a component of the likelihood gradient may be both noisy and inaccurate depending on the choice of perturbation scale. In the worst case, different perturbations may be needed for different components. Sensitivity based gradient computations can resolve the problem.
Software
The developed methods have been implemented, verified, and benchmarked in Mathematica. FCC is collecting methods and tools for advanced modeling and simulation for drug discovery and development in a software platform with the aim to provide easy access to efficient and robust methods for dynamical mixed effects modeling.
Collaborating partners: Prof. Johan Gabrielsson, Swedish University of Agricultural Sciences, Prof. Bert Peletier, Leiden University, Christine Ahlström, AstraZeneca